Optimization II

Linear Programming

Notes from .

Introduction

• Objective and constraint are linear
• Standard form: \(min \quad c^Tx \\ subject \> to \quad Ax = b \\ and \quad x \geq 0,\)
• Here $A$, $b$, and $c$ are fixed real constants and the we are finding $x$.
• If problem has only inequalities, can use slack variables to turn inequalities into equalities, and giving the slack variable $y$ nonnegative inequality (will turn problem back into standard form).
• Free variables method:
  • Replace variables with no non-negative constraint with non-negative inequality constrained variables (ex: $x_1 = u_1 - v_1$)
• Substitution method

Basic Solutions

\(Ax = b\)

• Take subset of linearly indep columns and create matrix $B$ (called basis) which is same rank as A.
• Assumption $dim(b) = m < dim(x) = n$ and rows of $A$ are linearly independent.
  • Dependency means either redunduncy or contraditions \(Bx_B = b\)
• Then $x = (x_B, 0)$ is the basic solution
• Under the assumptions, the system will always have at least one basic solution.
  • If one of the variables in $x_b$ is 0 then the solution is degenerate
• $x$ is said to be feasible if it satisfies the standard form (and basic feasible if it satisfies the above assumptions)

Fundamental Theorem of Linear Programming

• Theorem: Given a linear program in standard form where $A$ is an $m \times n$ matrix of rank $m$:
  1. If there is a feasible solution, there is a basic feasible solution
  2. If there is an optimal feasible solution, there is an optimal basic feasible solution.
• This theorem reduces the search space of the linear program to that of searching over basic feasible solutions.
  • At max basic solutions depend on the corresponding number of ways of selecting $m$ of $n$ columns.

Relations to convexity

• Theroem (Equivalence of extreme points and basic solutions): Let $A$ be an $m \times n$ matric of rank $m$ and $b$ an $m$-vector. Let $K$ be the convex polytopes of all $n$-vectors $x$ satisfying the standard linear program. A vector $x$ is an extreme point (vertex) of $K$ if and only if $x$ is a basic feasible solution.
  • IMP Collarary:If there is a finite optimal solution to the linear program, there is a finite optimal solution which is an extreme point of the constrained set.
• Why this works? Intuition
  • Linear Constraints define a polytope
  • Each basic solution corresponds to the extreme point (vertex) of the polytope.
  • Each optimal feasible solution has an optimal basic feasible solution
  • Hence, traverse the vertex to get your optimal solution!
  • Graphically, since objective is linear, min/max it will move it in a particular direction, so the optimal value within the constraint would lie in on the extreme point of the direction of min/max.
  • Refer to Figure below for more clarity

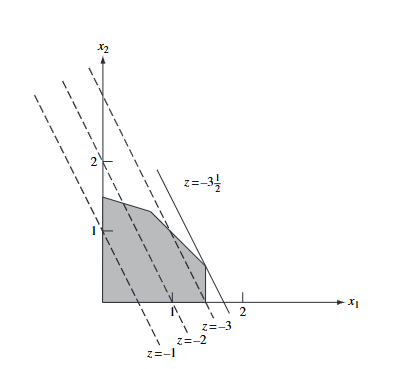
Figure 1: Global Solution at extreme point visualization.

Simplex Method

Pivots

For: \(Ax = b\)

• Switiching from one basic variable to a non-basic variable.

• A pivot is basically switching a basic variable to a non-basic variable, and vice versa (in the canonical form) to obtain a different basic solution.
• The new system of equation in canonical form has the following coeffecient for non-basic variables:

\[\begin{cases} y'_{ij} = y_{ij} - \frac{y_{pj}}{y_{pq}} y_{iq}, & \text{if } i \neq p \\[0.5em] y'_{pj} = \frac{y_{pj}}{y_{pq}} & \end{cases}\]

Where $x_p$ is the old basic variable and $x_q$ is the new basic variable.

The new basic solution would be the resulting $b’$ on the right side after transforming to the new canonical form.

Adjacent Extreme Points

• Only necessary to consider basic feasible solutions to the system when solving linear program
• Pivot operations takes one basic solution into another
  • Special conditions must be satisfied in order that a pivot operation maintains feasibility (nonnegaitvity of solution is not guranteed to be preserved by pivor operation)
• Make non-degeneracy assumption:
  • Every $x_i > 0$ in the basic solution
• How to gurantee feasability?
  • Selecting the right pivot element/vector (the element $p$ you want to replace with $q$)
  • After selecting the right pivot, apply the pivot operation
• How to select the right pivot? \(\varepsilon = \min_{i} \left\{ \frac{x_i}{y_{iq}} : y_{iq} > 0 \right\}\)
  • Right $p$ is at index $i \in m$ for the following equation \((x_1 - \epsilon y_{1q})a_1 + (x_2 - \epsilon y_{2q})a_2 + ... + (x_m - \epsilon y_{mq})a_m + \epsilon a_q = b\)
  • Where you are trying to replace one of the $m$ basis ($a_i$) with a new non-basic vector $a_q$.
  • If no $y_iq$ are positive, then it leads to a special case with unbounded feasible solutions.
  • Adjacent extreme points are points that lie on a common edge.
    • This method gives you one of the adjacent extreme points.
    • Reason being you are switching out one of the $x_i$ in $m$ for another one in $n-m$ so only one dimension is changing.
  • Geometrical Interpretations
    • Activity space: most intuitive
      • Where vector $x$ is represented (the dimensions of the graphs equal $dim(x)=n$).
      • Space where constraints cut of space and x must lie inside the cutout polytope
      • Pivoting here means you jump from one pivot to an adject neighbouring extreme point
        • As only one basis (constraint) is replaced with another.
        • You are moving along the edge.
    • Requirements space:
      • Where vector $a_i$ and $b$ are represented (the dimensions of the graph is $dim(a) = m$).
      • b is the positive linear combination of the $a$ vectors
      • Only certain combo of the basis can have a positive linear combination which gives b
      • And that is determined by our selecting pivot operation

Determining a minimum feasible solution

• This step will allow us to select the column so that the basic solution is feasible AND has a lower value to the objective function that the previous one.
  • Final step to get the simplex method
  • From previous step we can determine which vector should leave the basis in order to maintain feasability.
• For a basic solution $x_B$ and an objective function $z = c_1x_1 +c_2x_2+…+c_nx_n$; the corresponding cost value is: \(z_0 = c_B^Tx_B\)
• Choosing a direction:
  • For a cost for $x$: $z = c_1x_1 +c_2x_2+…+c_nx_n$
  • Substitute out $x_m$: \(\begin{aligned} x_1 &= y_{10} - \sum_{j = m+1}^n y_{1j} x_j \\ x_2 &= y_{20} - \sum_{j = m+1}^n y_{2j} x_j \\ &\,\vdots \\ x_m &= y_{m0} - \sum_{j = m+1}^n y_{mj} x_j \end{aligned}\)
  • Restulting equation: \(z = \mathbf{c}^T \mathbf{x} = z_0 + (c_{m+1} - z_{m+1}) x_{m+1} \quad + (c_{m+2} - z_{m+2}) x_{m+2} + \cdots + (c_n - z_n) x_n\)
  • Interpretation:
    • KEY: Think of $x_m$ as knobs to turn, which column to take as pivot, which direction you want to go to. The one which reduces the most make that as part of the new basis.
    • Can think of it discretely (hopping between adjacent extreme points) or continously.
• Theorem (Improvement of basic feasible solution): Given a nondegenerate baic solution with cost $z_0$, suppose for some $j$ holds $r_j = c_j-z_j < 0$.
  • Then there is a feasible solution with objective value $z < z_0$
  • If column $a_j$ can be subbed in to the basis for some other vector in it to get a new basic feasible solution, this new sol. will have $z < z_0$.
  • If $a_j$ cannot be subbed to yield a basic feasible solution, then set K is unbounded and the obj function can be made arbitrarily small towards minus infinity. Optimality Condition: If for some basic feasible sol $c_j-z_j \geq 0$ for all $j$, then that solution is optimal.

Simplex Method

1. For a tableau corresponding to a basic feasible solution. The relative cost coeff $r_j$ can be found by row reduction
2. If each $r_j \geq 0$ stop, the current basic feasible sol is optimal.
3. Select $q$ such that $r_q < 0$ to determine which nonbasic variable is to become basic.
4. Calculate the ratios $y_{i0}/y_{iq}$ for $y_iq \geq 0, i = 1, 2, …, m$.
   • If no $y_{iq} > 0$: the problem is unbounded and stop.
   • Otherwise, select $p$ as the index $i$ corresponding to the minimum ratio.
5. Pivot on the $pq$-th element, updating all rows including the last. Return to step 1.

The process terminates only when optimality is reached or unboundedness is discovered.

• Since there are only finite number of basic solutions, and no basis repeats because of strictly decreasing objective, the algorithm must reach a basis which is optimal or unbounded.

Artificial Variables

• Finding the first basic feasible solution
  • Sometimes very easy to find if slack variables are used.
  • Lot of times not very apparent:
    • Need an auxiliary linear program with simplex method applied to find the initial solution
• Artificial Minimization Problem