World Models

Introduction

• World Models are an explicit way to represent agent’s knowledge about it’s enviornment.
• When inputs are high-dim images, latent dynamics model predict ahead in an abstract latent space.
  • predicting compact representations instead of images has been hypothesized to reduce acculating errors, and can be parallelized due to its low compute footprint.
• Leant from a database of past experience
  • THe actor and critic on top is learnt from imagined sequences of compac model states

Dreamer V2

• Learn a World Model from past experience, use the world model for RL using Actor-Critic
  • RL in the model
  • Do rollout inside the model to refine and train the Actor-Critic
• Uses discrete latent representations (instead of continous) and balancing terms within KL loss.

World Model learning

• Arch: image encoder, recurrent state-space model (RSSM) to learn the dynamics, predictors for image, reward and discount factor.
  • RSSM uses a sequence of deterministic recurrent states $h_t$.
  • The posterior state $z_t$ has info about the current image, while prior state $\hat{z_t}$ aims to predict posterior without access to current image.
• All the components are implemented as Neural Networks.
  1. Reccurent model: $h_t = f_\phi(h_{t-1}, z_{t-1}, a_{t-1})$
  2. Representation model: $z_t \sim q_\phi(z_t \mid h_t, x_t)$
  3. Transition predictor: $\hat{z_t} \sim p_\phi(\hat{z_t} \mid h_t)$
  4. Image predictor: $\hat{x_t} \sim p_\phi(\hat{x_t} \mid h_t, z_t)$
  5. Reward Predictor: $\hat{r_t} \sim p_\phi(\hat{r_t} \mid h_t, z_t)$
  6. Discount Predictor: $\hat{\gamma_t} \sim p_\phi(\hat{\gamma_t} \mid h_t, z_t)$

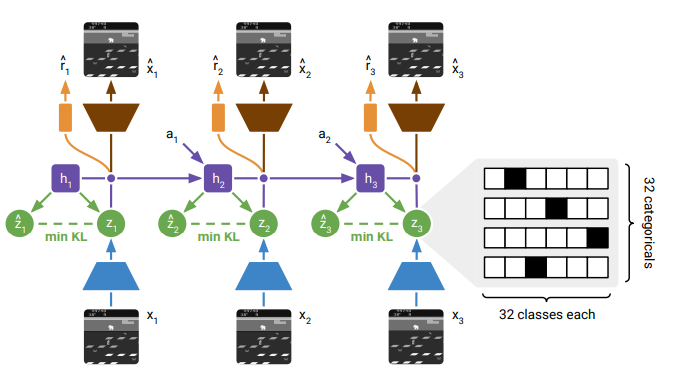
Figure 1: World Model Learning.

• Figure 1 shows how the Dreamer to components interact with each other.
• The transition predictor guesses the next model state without using the next image, so we can learn behavior by predicting model states without having to interact with the enviornment and observe images.
• The discount predictor allows for estimating probability of an episode ending.
• Model state is a concatenation of the deterministic $h_t$ and $\hat{z_t}$.
• ELBO loss function used to jointly optimize all components of the world model: \(\mathcal{L}(\phi) = \mathbb{E}_{q_t(\tau_t | \gamma_t, x_T^\pi)} \left[ \sum_{t=1}^T -\ln p_\phi(\sigma_t | h_t, z_t) - \ln p_\phi(r_t | h_t, z_t) - \ln p_\phi(\gamma_t | h_t, z_t) + \beta \text{KL}[q_\phi(z_t | h_t, x_t^\pi) \| p_\phi(z_t | h_t)] \right]\)
  • Uses KL-Balancing:
    • Make the prior match the representation while at the same time make the representation resemble the prior
    • Which should get the preferance?
      • Minimize KL loss faster with resepect to prior than the representations. This will avoid regularizing the representations to a poorly trained prior.
      • Use different learning rates $\alpha$ for prior and $1-\alpha$ for the approximate posterior.
      • This encorages learning an accurate prior over increasing posterior entropy.

Behavior Learning

• DreamerV2 learns long-horizon behaviors purely within its world model using an actor and a critic.
• Both actor and critic operate on top of the learnt model states
• The world model is fixed during behavior learning, so actor and value gradient do not affect it’s representations.
• Not predicting images allows for simulating 1000s of latent trajectories in parallel on a single GPU.

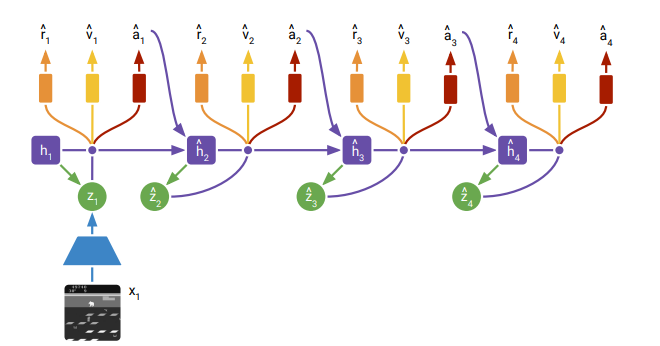
Figure 2: Behavior learning of actor-critic in the model latent states.

• Imagination MDP:
  • The diagram of the training within the imagination of the world model is as follows. Time horizon is finite (around 15 timesteps).
  • In this figure, trajectories start from posterior states computer during model training and predict forward by sampling actions using the actor network
  • The critic learns to predic the expected sum of future rewards for each state based on actors policy.
    • Use TD learning on imagined rewards
    • Actor is trained to maximize the critic prediction, via policy gradients.
  • Stochastic actor (for exploration) and deterministic critic: \(\hat{a_t} \sim p_\psi(\hat{a_t} \mid \hat{z_t})\) \(v_\epsilon(\hat{z}_t) = E_{p_\phi, p_\psi}[\sum_{\tau \geq t}\hat{\gamma}^{\tau-t}\hat{r}_t]\)
  • Latent state is markovian, so no need for conditioning on actor critic.
  • Trained from same trajectories but different loss functions for both.
  • Actor outputs categorical distribution over actions, critic has deterministic output.
  • Both are MLP NNs.
• Critic Loss Function:
  • TD learning used (n target steps used instead of 1), defined recursively.
  • Squared Loss is then optimized:
• Actor Loss Function:
  • Straight through gradient used (due to categorical latents and actions) along with REINFORCE gradients

Latent Diffusion Planning for Imitation Learning

• Learn a (video) planner and inverse dynamics model
  • Planner benifits from action-free data
  • IDM can used unlabelled suboptimal data
• Operates across images
• Forceast a dense trajectory of latent states
• Latent Diffusion Planning
  • Train a VAE with image reconstruction loss for latent embedding
    • Used by planner and IDM
  • Learn a Imitation Learning policy through:
    1. a planner: takes in demonstration state sequences which maybe action free
    2. IDM: trained on in-domain (possibly suboptimal) env interactions.
  • Diffusion used for both planner (forecast) and IDM (extract actions)
• Diffusion models conditioned on additional context:
  • Diff policy is conditioned on visual observations
  • Decision Diffuser can be conditioned on reward, skills and constraints.
  • Diffusion model also trained on latent space, so conditioned on $z$ instead of visual observations/
• Key point: encoder trained seperately (on action-free data too) and planner trained sepereatly on top of the encoder and it forecasts states (rather then just actions).
  • IDM requires action data (and suboptimal data would work too)
• Great for low-demonstration data imitation regime

Self-supervised world models

• Data collection is expensive
  • Not ideal to keep collecting data for each new task
  • explore enviornment once without reward to collect diverse dataset
    • useful for any downstream task
    • in downsteam task only reward funtion given and no further enviornment interaction for training
  • Called task agnostic RL
• Intrinsic Motivation
  • to explore complex enviornments in absence of reward, agent needs “intrinsic motivation”
  • ex: seek input it cannot predict accurately
    • visit rare states
    • curiosity based exploration (read paper, important)
• Plan 2 Explore (this paper):
  • Learn world model to plan ahead and seek out expected novelty of future situations.
    • Learn exploration policy purely from imagined model states without enviornment interactions.
      • Policy optimized from imagined trajectories to max intrinsic reward.
    • Challenge: train an accurate world model and define an effective exploration objective.
      • GOod objective is one that seeks input that agent can learn most from (epistemic uncertainty) while being robust to stochastic part of env that cannot be learn like noise (aleatoric uncertainty).
  • Use ensemble of model to predict next state dynamics for a given state and action
    • the variance is equal to the reward
    • the higher the variance means the model is not sure about that state action pair (called the disagreement objective).
      • the disagreement is positive for novel states
      • given enough samples, it eventually reduces to zero (not novel now) even for stochastic enviornments because all converge to the mean of the next input (hence gets rid of aleatoric uncertainty).
  • Use dreamer as world model
    • First-phase: Use the default actor-critic to explore the world model but with the disagreement objective in the world model imagination.
      • Execute the exploration policy in the enviornment to expand the dataset (initially a few random epsiodes on which the world model and the ensemble was traine on)
    • Second-phase: agent is a given a downstream task in form of a reward function; should adapt with no env interaction.
• Quantifying uncertainty is an open problem in DL
  • Ensemble disagreement is one empirical method

There is no turning back: A self-supervised approach for reversibility-aware reinforcement learning

• Irreversible outcomes are usually regretful actions and dangerous
• Irreversibility as a prior and self-supervised signal for exploration; leads to safer behaviors.
  • Also, leads to more efficent exploration in enviornments with undesirable irreversible behaviors
  • Tested on Sokoban puzzle game
• Estimating reversibility is hard
  • Needs causal reasoning in large dimensional spaces
  • Instead, learn in which direction time flows between two obervation from agents’ experience
    • Consider transitions irreversible that are assigned a temporal direction with high confidence. KEY POINT
    • Reversibility here a simple classification problem of predicting temporal order of events
    • Still not good!
• Approximating reversibilit via temporal order
  • Learn temporal order in a self-supervised way through binary classification of sampled pairs of observation from trajectories.
• Reachability and reversibility are related.
• Reversibility is good for safe exploration

Reversibility

• Degree of reversibility of an action: \(\phi(s,a) := sup_\pi p_\pi (s \in \tau_{t+1:\infty} \mid s_t = s, a_t =a)\)
• In determinsitic env, action (take in $s$ to reach $s’$) is either reversible or irreversible. Hence $\phi_K(s,a) = 1$ if there is a sequence of less than K actions which brings the agent from $s’$ to $s$, and is otherwise 0. For stochastic env, a given sequence of actions can only reverse a transition up to some probability, hence degree of reversibility.
• Policy dependent reversibility: remove $sup$ from the above equation. \(\phi_{\pi, K}(s,a) := p_\pi (s \in \tau_{t+1:t+K+1} \mid s_t = s, a_t =a)\)

Reversibility estimation via classification

• estimating precedence: basically which state comes first on average $s$ or $s’$. Train a precedence estimator which using a set of trajectories learns to predict which state of an arbitrary pair is most likely to come first.
• finite precedence estimator: \(\psi_{\pi,T}(s,s') = \mathbb{E}_{\tau ~ \pi} \mathbb{E}_{s_t=s, s_{t'}=s'}[\mathbb{1}_{t'>t}]\)
  • given two states $s’$ and $s$, the precediance estimator gives an approx. probability of $s’$ being visited after $s$.
• Empiracal reversibility using precedence estimator: \(\bar{\phi}_\pi (s,a) = \mathbb{E}_{s' ~ P(s,a)}[\psi_\pi (s',s)]\)

Temporal Difference Learning for Model Predictive Control (TD-MPC) <d-cite key”hansen2022temporal”></d-cite>

• Costly to plan over long horizons
• Challenging to obtain accurat model of enviornment
• Using an internal model of the enviornment, agent can plan ahead of time
• Contribution: how the model is learned.
  • learn the latent represenation of the dynamics from rewards only (no state/image prediction).
  • back-propagate gradients from the reward and TD-objective through multiple rollout steps of the model.
    • improves long horizon predictions
  • modality-agnostic prediction loss in latent space
    • enforces temporal consistency w/o state/image prediction.
• Tested on DMControl and Meta-World
• Primarily focused on dense rewards it feels like
• Uses MPPI control for planning, learns a model for the latent dynamics and reward signal and a terminal state-action value function.
  • Terminal value used in finite horizon planning, refers to the value of the state if followed how much expected rewards will be gained.
  • MPPI is an MPC algorithm that iteratively updates parameters for a family of distributions using and importance weighted average of the estimated sampled trajectories. Usually, fit parameters of a time-dependent multivariate Gaussian with diagonal covariance.
  • Basically, steps as follows:
    1. Rollout $N$ trajectories
    2. Estimate the expectated rewards for each
    3. Select top $k$
    4. Calculate the “optimal” estimate using some form of weighted average
    5. Select the first action, and plan again
  • This is called a “feedback policy”
  • Warm start by reusing the next timestep value from previous run.
  • Constrain variance so it is not too low to avoid local minimas.
  • Also, have a “guide policy” which helps with exploration.
    • Add addtional samples from this policy to the planning procedure.

Task-Oriented Latent Dynamics Model

• Jointly learnt with terminal value function using TD-learning.
• TOLD model only learns to modle elements of the env that are predictive of the reward.
  • TrajOpt using TOLD for estimating short-term reward using rollouts, and long-term returns using terminal value function.
• Apparently, supports continuous action spaces adn sparse reward signals.
• World Model implemeted as purely deterministic MLPs (without RNN gating or probabilitic models).
• Loss includes reward, long term value, and latent state consistency.
• Latent state consistentcy loss: predicted and ground truth latent states should be similar (rather then output observations).

Learning Latent Dynamics for Planning from Pixels

• OG paper about learning dynamics from interaction with the world
• Deep Planning Network (PlaNet)
  • Model based agent that learns the env dyamics from images and chooses actions through onlin planning in latent space.
• Dynamics model must accurately predict rewards ahead multiple time step
  • Latent dynamics model
• Solve tasks from DM Control
• Recurrent state space model
• Latent overshooting objective

Latent Space Plannning

• assume learned dynamics model
  • planning within this model
• consider a partially observable markov decision process (POMDP) setup.
  • define a transition func, observation func, reward func, and a policy.
• model-based planning
  • use MPC, replan at each step, within this latent space defined by the transition func and an encoder.
  • no model-free RL algorithms used
• experience collection
  • need to iteratively collect new experience and refine dynamics model (exploration phase).
    • do this by planning with partially trained model
    • update the model and repeat
    • add gaussian noise to make it more robust.
• planning algorithm:
  • use cross-entropy method to search for best action sequence.
  • CEM is a population based opt algorithm that infers a distribution over action sequences that maximize the objective.
    • similar to TD-MPC, sampling based it seems
    • research more on Cross entropy method (CEM)
      • based on importance sampling

Recurrent State Space Model (RSSM)

• can be though of as a non-linear Kalman filter or sequential VAE.
• deterministic vs stochastic mode
  • stochastic mode is Gaussian with mean and variance
• RSSM splits the stochastic and deterministic parts
  • transition of RNN are deterministic
  • state model, observation model, reward model also deterministic
  • refer to paper for the diagram
• transitions are not stochastic as it makes it difficult to remeber information over multiple time steps

Latent Overshooting

• trains all multi-step predictions in latent space
  • use latent space variables, no need to generate additional images
• latent overshooting is a regularizer in latent space which encourages consistency between one-step and multi-step predictions.
  • look more into derivations