Policy Optimization and Actor Critic Methods

Policy Optimization

• Learn policy directly from enviornment
• Stochastic policy class smooths out the optimization problem
• Optimize the following: \(max_\theta E[\sum^H_{t=0}R(s_t) \mid \pi_\theta]\)
• Policy optimization can be simpler then $Q$ or $V$
  • V doesn’t have transition
  • argmax over actions for Q often difficult for continous actions

Likelihood Ratio Policy Gradient

• Goal is to find max expected reward over a policy: \(max_\theta U(\theta) = max_\theta \sum_\tau P(\tau; \theta)R(\tau)\)
• Where:
  • Total reward: $R(\tau) = \sum_{t=0}^HR(s_t, u_t)$
  • $\tau$ is a state action sequence upto timestep $H$
• Goal is to favor trajectories with higher reward
• Gradient based optimization:
  • Sample based approximation
  • $\frac{\nabla_\theta P(\tau, \theta)}{P(\tau; \theta)} = \nabla_\theta log P(\tau; \theta)$
  • $\nabla U(\theta) = \hat{g} = \frac{1}{m}\sum_{i=1}^m\nabla_\theta log P(\tau^i; \theta)R(\tau^i)$
  • Can be used no matter what the reward function is (discontinuous/unknown)
  • Only derivative with respect to the trajectory distribution
  • Probability distribution over trajectories is inducing trajectories, so we can still take gradients! IMPORTANT POINT
• Intuition:
  • Gradient tries to inrease probability of paths with positive R
  • Decrease probablity of paths with negative R

Temporal Decomposition

• No dynamics model required for gradient update \(\nabla_\theta log P (\tau^i; \theta) = \sum_{t=0}^H\nabla_\theta log \pi_\theta(u_t^i \mid s_t^i)\)
• Get gradients from backpropagration, do rollouts and estimate $\hat{g}$
• But estimates unbiased but very noisy

Actor-Critic Methods

• Modification to Policy Optimizations that make it actor-critic

Baseline subtraction

• Subtract baseline $b$ from total reward
• Rewards from the past are not relevant, so those can be remove from the estimate
• Removing terms that don’t depend on current action can lover variance:
• New estimate: \(\frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{H-1} \nabla_\theta \log \pi_\theta(u_t^{(i)}|s_t^{(i)}) \left( \sum_{k=t}^{H-1} R(s_k^{(i)}, u_k^{(i)}) - b(s_t^{(i)}) \right)\)
• Good choice for $b$:
  • constant baseline which is average of trajectory rollouts
  • Minimum variance baseline: take weighted average, resulted in lower variance, not seen much in implementation
  • Time-dependent baseline
  • State-dependent expected return: essentialy learning the value function of states.
    • Per state you have a different $b$ in the gradient estimate.
• Increase logprob of action proportionally to how much its returns are better than the baseline (expected return) under the current policy.
  • The state dependent baseline (value function) is most intutive to understand this. (This is the critic and the policy network is the actor)
• Need to learn this value function
• $R_t-b(s_t)$ is also usually called the advantage estimate or $\hat{A_t}$.

Value Function Estimation

• Monte Carlo Estimation of $V^\pi_\phi$, regress against empirical return: \(\phi_{i+1} \leftarrow \arg\min_\phi \frac{1}{m} \sum_{i=1}^{m} \sum_{t=0}^{H-1} \left( V_\phi^\pi(s_t^{(i)}) - \left( \sum_{k=t}^{H-1} R(s_k^{(i)}, u_k^{(i)}) \right) \right)^2\)
• Can also do bootstrapping instead:
  • Do a fitted value iteration \(\phi_{i+1} \leftarrow \min_\phi \sum_{(s,u,s',r)} \|r + V_\phi^\pi(s') - V_\phi(s)\|_2^2 + \lambda\|\phi - \phi_i\|_2^2\)

Advantage Estimation

• Variance reduction by function Approximation (and discount factor)
  • approximate average reward by some steps of reward plus value function from that timestep onwards
• Trading off for low variance and introducing high-bias, can to n-step estimate (similar to TD (lambda)).
• Gradient estimate for $V$:

\[\phi_{i+1} \leftarrow \min_\phi \sum_{(s,u,s',r)} \|\hat{Q}_i(s,u) - V_\phi^\pi(s)\|_2^2 + \kappa\|\phi - \phi_i\|_2^2\]

• Gradient estimate for $\pi$:

\[\theta_{i+1} \leftarrow \theta_i + \alpha \frac{1}{m} \sum_{k=1}^{m} \sum_{t=0}^{H-1} \nabla_\theta \log \pi_\theta(u_t^{(k)}|s_t^{(k)}) \left( \hat{Q}_i(s_t^{(k)}, u_t^{(k)}) - V_{\phi_i}^\pi(s_t^{(k)}) \right)\]

General structure of algorithm:

1. Init $\pi_{\theta_0}, V^\pi_{\phi_0}$
2. Collect Rollouts ${s, u, s’, r}$ and $\hat{Q}_i(s,u)$
3. Update :
   • \[\phi_{i+1} \leftarrow \min_\phi \sum_{(s,u,s',r)} \|\hat{Q}_i(s,u) - V_\phi^\pi(s)\|_2^2 + \kappa\|\phi - \phi_i\|_2^2\]
   • \[\theta_{i+1} \leftarrow \theta_i + \alpha \frac{1}{m} \sum_{k=1}^{m} \sum_{t=0}^{H-1} \nabla_\theta \log \pi_\theta(u_t^{(k)}|s_t^{(k)}) \left( \hat{Q}_i(s_t^{(k)}, u_t^{(k)}) - V_{\phi_i}^\pi(s_t^{(k)}) \right)\]

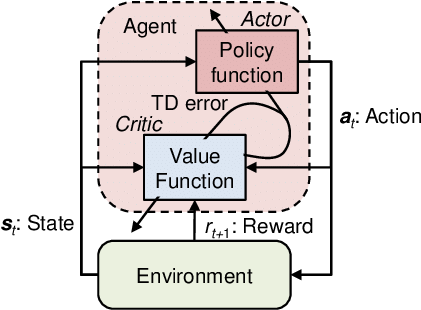
Figure 1: Actor-Critic Algorithm.